The total energy of an orbiting body or satellite – equation derivation with sample numerical

Last updated on January 25th, 2022 at 08:50 pm

In this post, we will derive the equation of the total energy of an orbiting body, and then will solve a numerical problem using the formula derived.

---

Derive the formula of the total energy of an orbiting body (or satellite)

To calculate the total energy of an orbiting body (say a satellite) we have to find out the sum of its kinetic energy and potential energy.

In one of our earlier posts, we have already seen how to derive the formula of the potential energy of an orbiting body.

The potential energy of an orbiting body can be expressed with the formula: PE = – GMm/r
Here, the mass of the orbiting body is m and the radius of its orbit is r. M is the mass of a planet.

Hence we can start with this now: Total Energy E = Potential energy + Kinetic energy = PE + KE = – GMm/r + (1/2)mv² ……….. (1)

Now, as the body in orbit is in a circular motion, hence its centripetal force is being supplied by the gravitational force between mass m and M.

mv²/r = GMm/r²

v² = GM/r ……………… (2)

Hence, KE = (½) m v² = (½) m [GM/r] = (½) [GMm/r] …………………….(3)

So, from (1) and (3):

E = PE + KE = – GMm/r + (½) m v² = – GMm/r + (½) [GMm/r] = – (Gmm)/(2r)

The total energy of an orbiting body or satellite E = – (Gmm)/(2r) ………………. (4)

So equation 4 above is a formula giving the total energy of an orbiting body. It will always be negative because there is always more negative potential energy than positive kinetic energy for an orbiting body.

Let’s do an example to see how this total energy changes in a change in orbit.

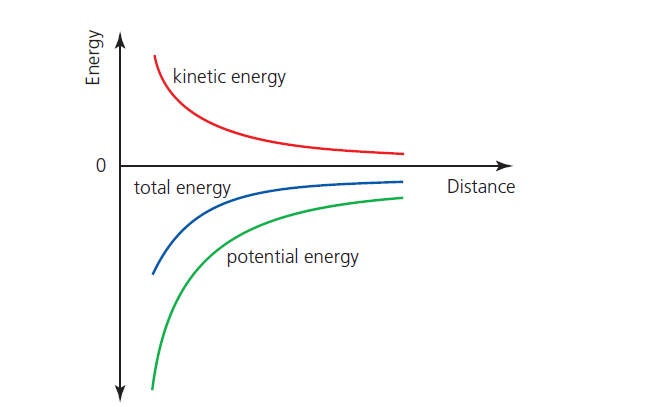
Orbital Energy – graphs

Figure 1 below shows three graphs representing the Potential energy of the satellite, the Kinetic Energy of the satellite, and the total energy of the satellite (total orbital energy).

Orbital energy – all formulas in a figure

---

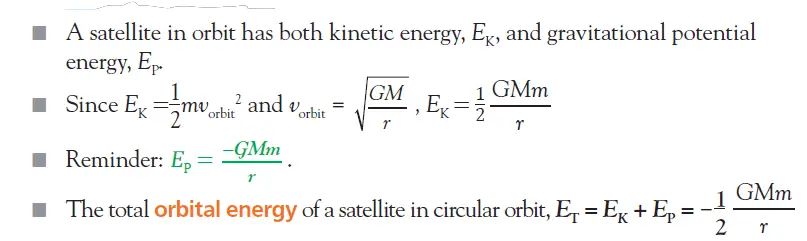
Numerical problem – solve using the formula of total energy of an orbiting body or satellite

Numerical Question: A 2,500 kg satellite is orbiting the earth with an orbital radius of 6,500 km. It moves to an orbit with an orbital radius of 10,000 km. Find the energy required to perform this adjustment.

Solution:

Mass of the earth M = 6.0 × 10²⁴ Kg

Mass of the satellite =m= 2500 Kg

r₁ = 6,500 x 10³ m

r₂ = 10000 x 10³ m

G = 6.67 × 10^–11

The energy required to perform the manoeuvre will be equal to the difference in energy before and after the change (i.e. conservation of energy). We have a formula for total energy, so:

ΔE = E_f -E_i = – (Gmm)/(2r₂) – [- (Gmm)/(2r₁)] = GMm/(2r₁) – GMm/(2r₂) = GMm[ 1/( 2r₁) – 1/(2r₂)]

After putting the values and calculating we get,

ΔE = 2.7 x 10¹⁰ J

Notice that this is a positive quantity, even though the energy at each point individually is negative – we do work to make the total energy less negative.