Surface tension equals the free energy of the liquid surface – prove it

Surface tension (S) equals the free energy (E) of the liquid surface (Temperature remaining constant).

Let’s see how we can prove that mathematically using an experimental setup.

how to prove that Surface tension equals the free energy of the liquid surface?

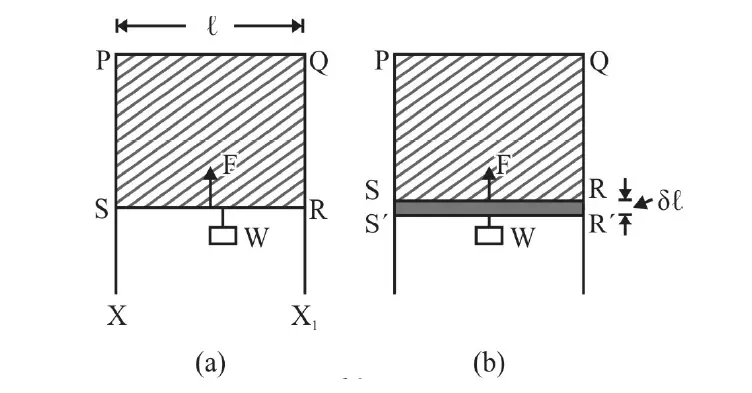
Figure 1 above shows a frame XPQX1 over which wire RS can slide without any friction.

Step 1

Form a liquid film of soap solution and place the arrangement in a vertical plane.

Wire RS starts moving vertically upwards! This is due to surface tension.

As wire RS move towards the side PQ area of film decreases. This means there is a vertically upward force, F, due to Surface Tension (S.T.) on RS.

Step 2

Suspend a small weight w from RS so that RS is in equilibrium.

Obviously, F = w.

Experiments show F is directly proportional to the length of RS i.e., l.

We write, the net force on RS due to surface tension as F = 2 S l, where S is a constant depending on the nature of the film. The factor of 2 in the above equation is due to the presence of two free surfaces.

Had there been only ONE free surface then, F = Sl

S is known as the surface tension of the liquid surface.

Definition: Surface tension is numerically equal to force per length acting along the liquid surface (i.e. a tangential force) at right angles to any arbitrary line on the liquid surface.

SI unit of Surface tension is Nm^–1 and its dimensions are MT^–2.

Step 3

In Fig. (b), wire RS is pulled down very slowly (so that surface film does not break) to position R’S’ by an infinitesimally small distance Δl.

The work done, dw, against the force of Surface Tension on RS = F× Δl = 2Sl × Δl.

Let E be the free energy per unit area of the liquid surface.

The work done dw is used to increase the free energy of the liquid surface.

Now, Increase in free energy = Additional area of the film created × E

= 2×area RR ‘SS’×E

= 2× l × Δl ×E

Step 4

From the law of conservation of energy

2Sl × Δl = 2× l × Δl ×E

or, S = E

In other words; when the temperature remains constant, surface tension (S) equals the free energy (E) per unit area of the liquid surface.

Summary

• Surface tension is numerically equal to force per length acting along the liquid surface (i.e. a tangential force) at right angles to any arbitrary line on the liquid surface.
• SI unit of Surface tension is Nm^–1 and its dimensions are MT^–2.
• When the temperature remains constant, surface tension (S) equals the free energy (E) per unit area of the liquid surface.