Excess pressure inside Liquid Drop and Liquid Bubble – derivation of equations

In this post, we will derive the equations for the Excess pressure inside Liquid Drop and Liquid Bubble.

Small-sized liquid drops and a bubble are spherical in shape due to surface tension.

The liquid surface is curved; therefore there is an excess pressure; p; inside the liquid drop or a bubble.

Liquid Drop – Excess pressure equation derivation

Consider a liquid drop of radius r, surface tension S as shown in Fig. Let p be the excess pressure inside liquid drop.

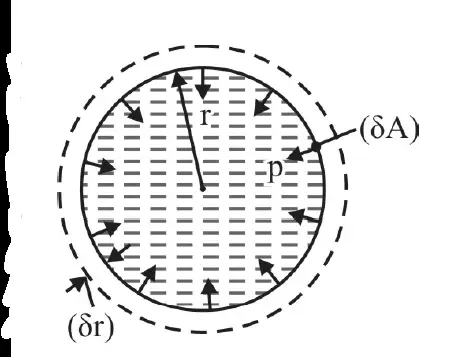
Very slowly we increase the radius of the drop to (r + dr). Work has to be done due to force because of excess pressure. Consider a small area dA on the surface of the drop.

Force on the area considered due to excess pressure = p.dA.

Work done against surface tension to increase the radius of drop by dr = (p.dA).dr.

The total work done, dW = Σ(p.dA).dr = p [ΣdA].dr = p.[4πr²] dr ……… (1)

[ ΣdA = Total surface area of liquid drop = 4πr² ]

The work done appears as an increase in the free energy dE of a liquid drop.

Obviously, dE = Increase in surface area × S = 4π [(r+dr)² – r²]x S = 8πrS.dr…..(2)

From law of conservation of energy, dW = dE

p.[4πr²] dr = 8πrS.dr

or p = 2S/ r …..(3)

Liquid Bubble – Excess pressure equation derivation

A liquid bubble has two free surfaces. Therefore excess pressure p = 4S/r ……… (4)