Numerical problems on Resistivity with solution
Last updated on August 25th, 2023 at 03:07 pm
This post presents a few important numerical problems in physics that you can solve using the concepts of resistivity. If you want a quick revision to memorize the resistivity formula then you can check this post on resistivity formula derivation.
Note: Remember that: (1) resistivity is a property of the material (2) the unit of resistivity is ohms times metres and not ohms per metre. (3) In calculations, l must be in metres and A must be in m2.
Resistivity – Numerical problems with solution
1 ] Question1
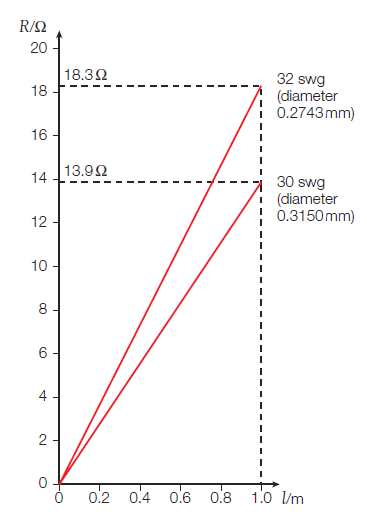
Use the data for the 32 swg wire given in Figure 1 to calculate a value for the resistivity of nichrome.
Solution: Answer
R = ρl/A
where A = π (d/2)2
Rearranging:
ρ = RA/l
Fetched data from Figure 1 for the 32 swg wire.
Substituting R = 18.3 Ω when l = 1.000 m and d = 0.2743 mm:
ρ = (18.3 Ω) π(0.5 × 0.2743 × 10–3 m)2 / 1 m = 1.08 × 10–6 Ω m
2 ] Question 2
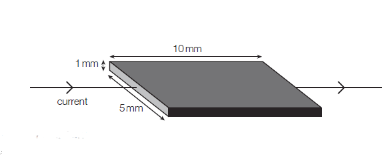
A carbon chip of resistivity 3.0x 10–5 Ω m has the dimensions shown in Figure 2.
What resistance does the chip have for a current in the direction shown?
Solution: Answer
Using the formula:
R = ρl/A
Referring figure 2 we get, l = 10 mm = 10 × 10–3 m
and A = 5 mm × 1 mm = 5 × 10–3 m × 1 × 10–3 m
= 5 × 10–6 m2
Resistance of the chip = R = ρl/A= ( 3.0x 10–5Ωm)(10 × 10–3 m) /5 × 10–6m2
=0.060 Ω
3 ] Question 3
A conductor wire of length 2.0 m and diameter 4 mm has a resistance of 16 Ω at room temperature. Find its resistivity. In your opinion, is the wire is made of pure metal or alloy?
Solution:
Length of wire, l = 2.0 m, diameter, d = 4 mm = 4 × 10-3 m.
So, the area of cross-section A = π d2/ 4.
The resistance, R = 16 Ω.
If ρ be the resistivity of the material of the wire, we have
R = ρ l / A,
which gives
ρ = R A / l = R π d2 / (4 l)
Or ρ = (16 Ω) (3.14) (4 × 10-3m)2 / (4 × 2.0 m) = 100.5 × 10-6 Ω m.
The above value of ρ tells us that the wire is made of alloy.
4 ] Question 4
A metallic wire has a radius of 0.25 mm and a resistance of 5 Ω. What will be the length of this wire if the resistivity of the material of the wire is 3.2 × 10-8 Ω m?
Solution
Radius r = 0.25 mm = 2.5 × 10-4 m.
Required resistance R = 5 Ω
Resistivity of the material of the wire ρ = 3.2 × 10-8 Ω m
Length of wire L =?
Now, the area of the cross-section of the wire A =π r2.
We have, R = ρL / A, which gives
L= R A / ρ = Rπ r2 /ρ
or, L = (5 Ω) × (3.14) × (2.5 × 10-4m) 2 / (3.2 × 10-8 Ω m)
=> L= 30.7 m.
So, the required length of wire L = 30.7 m.
