How to deviate light rays by 180 degrees with a prism?
Last updated on April 13th, 2021 at 10:19 pm
Let’s see how a light ray can be deviated by 180 degrees with the help of a prism. A total reflecting prism is used here to get a 180-degree deviation of a light ray.
Conditions to get a 180-degree deviation of a light ray with a prism
Conditions are as follows to get a deviation of 180 degrees:
1 ] requirement of a Total reflecting prism (right-angled isosceles prism with a 90-degree angle between two equal sides, and 2 more angles with 45 degrees each)
2 ] Light is to be incident normally on that specific side of the Total reflecting prism (right-angled isosceles prism) that makes 45 degree angle with each of the other 2 sides.
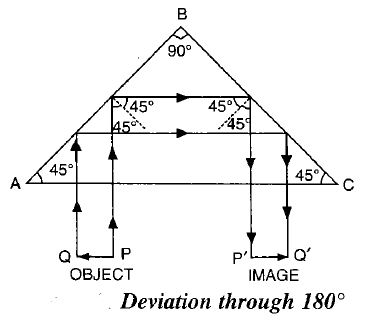
In the above diagram, take a light ray PQ incident on AC normally (making a 90-degree angle with AC).
With no deviation, it comes inside the prism and hits the AB with a 45-degree angle of incidence, which is more than the critical angle for the air-glass pair (42 degrees).
Hence the ray of light suffers a total internal reflection at surface AB.
As a result, it gets totally reflected internally and again hits the side BC inside the prism with a 45-degree angle of incidence again. Obviously here also total internal reflection happens.
The totally reflected ray now hits again the side AC inside the prism normally (90 degrees with AC) and comes out of the prism to air without any more deviation at AC.
It is evident that the ray of light gets deviated twice, once by 90 degrees after it hits the AB side, and then it gets deviated by 90 degrees once more after hitting side BC.
Thus we get a total 180-degree deviation of the light ray with a prism.
