How to deviate light rays by 90 degrees with a prism?

Last updated on April 13th, 2021 at 10:21 pm

Let’s see how a light ray can be deviated by 90 degrees with the help of a prism. A total reflecting prism is used here to get a 90-degree deviation of a light ray.

In the next section, we have enlisted the conditions to be satisfied to get that deviation.

Conditions to get a 90-degree deviation of a light ray

Conditions are as follows to get a deviation of 90 degrees:

1 ] requirement of a Total reflecting prism (right-angled isosceles prism with a 90-degree angle between two equal sides, and 2 more angles with 45 degrees each)

2 ] Light is to be incident normally on either of the two equal sides of the Total reflecting prism (right-angled isosceles prism)

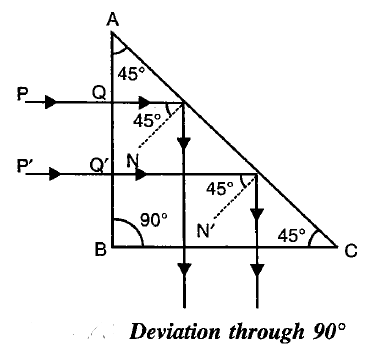
In the above diagram, take a light ray PQ incident on AB normally (making a 90-degree angle with AB).

With no deviation, it comes inside the prism and hits the AC with a 45-degree angle of incidence, which is more than the critical angle for the air-glass pair (42 degrees).

Hence the ray of light suffers a total internal reflection at surface AC. As a result, it gets totally reflected internally and deviated by 90 degrees at the AC.

Then it falls on the BC of the prism normally again(so the angle of incidence of the light ray is zero on BC) and hence it comes out of the glass prism to the air with no more deviation at BC.

Thus we get a 90-degree deviation of the light ray with a prism.