Internal Resistance of a Cell - definition, formula, diagram

Last updated on June 23rd, 2023 at 02:08 pm

What is the Internal Resistance? | Define the internal resistance of a cell

All electric cells are made of materials that have resistance. The resistance of the cell is called the internal resistance.

Not all of the chemical energy converted to electrical energy inside a cell emerges at the terminals of the cell.

When a charge flows and produces a current in the cell, some of the energy is used up in ‘pushing’ the electrons through the cell. In other words, it is used to overcome the internal resistance of the cell, which is usually given the symbol r.

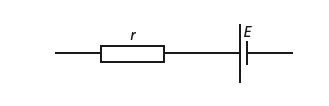
How internal resistance of a cell affects the current flow in a circuit

If a cell with internal resistance is connected to a resistor, the current will flow from the cell.
As current flows through the internal resistance, some energy is converted from electrical to heat inside the cell (so the cell gets hot). That results in a potential drop across the internal resistance of the cell.
This means that there is less energy to be converted to heat in the resistor. The potential difference (p.d.) across the resistor is therefore less than the emf of the cell.

Internal Resistance Formula

Consider a cell of e.m.f., ε, and internal resistance, r, which is connected to
a lamp of resistance, R, as in Figure below.

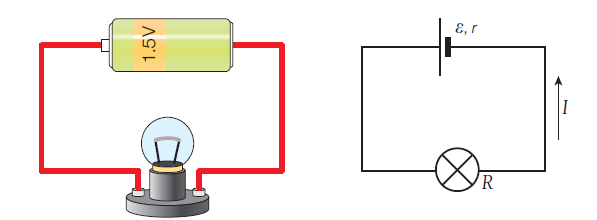
If there is a current, I, in the circuit:

rate of energy converted in cell = rate of work done against internal resistance + rate of work done lighting lamp

=>εI = I²r + I²R
=>ε = Ir + IR ……………… (1)
=> I = ε / (R+r) ……………. (2) [Equation of current]
=>r = (ε – IR)/I ……………… (3) [Internal resistance formula]

Internal resistance formula
r = (ε – IR)/I

The internal resistance of a battery or cell – a visual representation

The internal resistance of a battery or cell - visual representation

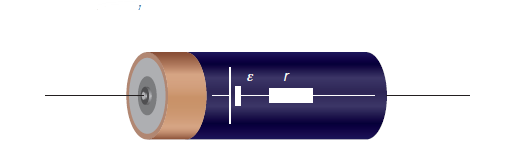
It is helpful to think of a power supply (such as a cell) as being a voltage (the e.m.f.) in series with a resistor (the internal resistance) as shown in the Figure above.

The internal resistance of the ideal voltage source is zero.

Numerical Question based on Internal Resistance (Practice problem)

Question) A torch battery of e.m.f. 4.5 V and internal resistance 0.4 Ω is connected across a lamp of resistance 6.4 Ω.
1) What is the current in the lamp?
2) How much power is:
(a) dissipated in the lamp
(b) wasted in the cell?

Solution:
(1)
Circuit current, I = ε/(R + r)= 4.5 V/(6.4 Ω + 0.4 Ω) = 0.66 A
(2a)
For power dissipated in the lamp:
P = I²R = (0.66 A)² × 6.4 Ω = 2.8 W
(2b)
For power wasted in the cell:
P = I²r = (0.66 A)² × 0.4 Ω = 0.2 W