Find the magnetic field B at the center of square loop of side a carrying a current I

In this post, we will find the formula of the magnetic field B at the center of a square loop of side a, carrying a current I.

Here is the diagram to understand the situation.

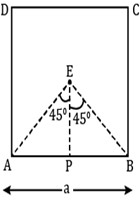
Solution:

E is the center of the square ABCD. Current I is flowing through ABCD.

the distance between the center E and the midpoint of AB =r = Length of  PE=a/2

Now, calculating the magnetic field at center E due to the current carrying AB side, we will use this formula,
B_AB=(μ₀I)(sinθ1+sinθ2)/(4πr)

B_AB=(μ₀I)(sin45^o+sin45^o)/(4πa/2)
=>B_AB=[(μ₀ 2 I)/(4πa)](√2)
=>B_AB=(μ₀ 2√2 I)/(4πa) ………….. (1)
Since all sides of the square create the same magnetic field at the center (the direction is also the same), so total magnetic field B will be
B=4×B_AB=4×(μ₀ 2√2 I)/(4πa)

∴B=8√2[(μ₀ I)/(4πa)] …………… (2)

Equation (2) can also be expressed as: B=2√2[(μ₀ I)/(πa)]