Prove that Refractive index = Real depth/apparent depth

Last updated on August 24th, 2023 at 12:46 pm

In this post, we will prove mathematically that Refractive index = Real depth/apparent depth.

As an Illustration of refraction: 1) When seen from outside, the bottom of a water body appears to be raised. This is due to refraction at the plane surface of the water. In this case, the Refractive index of water n = Real depth/apparent depth.

This relation holds good for a plane parallel transparent slab also, as shown below.

Refractive index = Real depth/apparent depth

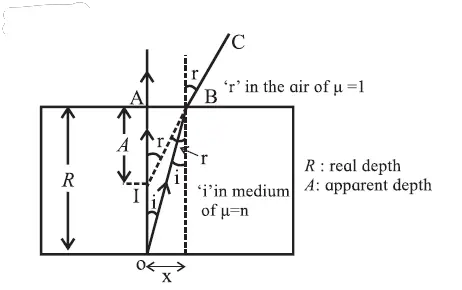
Figure 1 shows a plane parallel slab of a transparent medium of refractive index n. A point object O at real depth R appears to be at point I at apparent depth A when seen from outside (air).

Incident rays OA (traveling undeviated) and OB (deviating along BC) are used to locate the image.

R = real depth, and A= apparent depth

By considering i and r to be small, we can write,

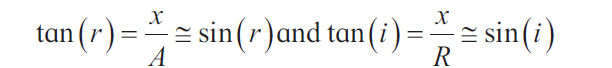
[According to one of the Laws of refraction, the Angle of incidence (θ1 in a medium of refractive index n1) and angle of refraction (θ2 in a medium of refractive index n2) are related by Snell’s law, given by
(n1)sinθ1 = (n2)sin θ2. ]

Using this we can write the following:

n sin(i) = 1. sin(r) [note that RI of air is taken as 1]

n = sin(r)/sin(i)

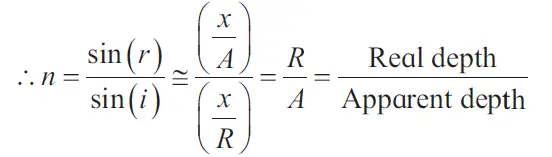
Thus we can prove that Refractive index = Real depth/apparent depth