Orbital motion of a charge in the magnetic field & radius of the orbit

The direction and magnitude of the force on a charged particle in a magnetic field affect the path that an electric charge takes. The direction of the force causes the charge to move in circles, and the force’s magnitude affects how big of a radius that circle has. In this post, we will discuss the orbital motion of charges in magnetic fields. We will also derive an equation of the radius of the circular path that an electric charge takes. In this study, we will also find the X and dot convention to understand the direction of the magnetic field.

X and dot convention to understand the direction of the magnetic field | X and .

In a magnetic field, the force on the moving charge is perpendicular to the direction of the travel.

To better show the path of the charge, physicists often draw the magnetic field as though we are looking at it straight on. How can we tell which way the magnetic field is going?

Here’s the physics way of showing direction using the X and dot convention:

Away from us: If we see a bunch of X’s, the magnetic field goes into the page. Those X’s are intended to be the end of vector arrows, seen tail-on (imagine looking down the end of a real arrow, tail toward you).

Toward you: Dots with circles around them are supposed to represent arrows coming at us, so in that case, the field is coming toward us.

Orbital motion of a charge in the magnetic field

Take a look at Figure 1, which shows the path taken by a positive charge moving in a magnetic field. The positive charge travels along a straight line, undeflected until it enters the magnetic field that goes into the page (represented by the X’s). Then a force appears on the charge at right angles, bending its path, as you can see in the figure below.

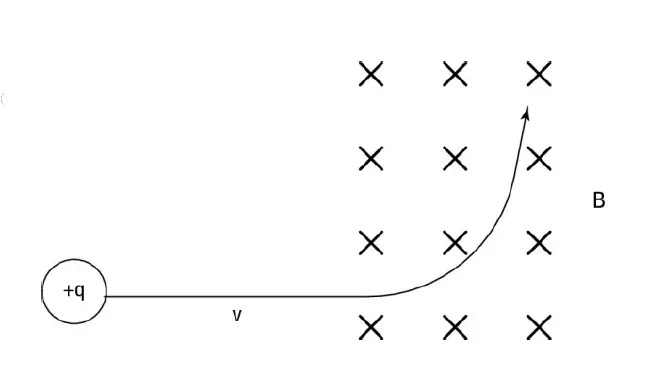
In the above figure, the magnetic field is always perpendicular to the direction of travel. And no matter which way the charged particle turns, the force on it is perpendicular to its motion. That’s the feature of circular motion: The force is always perpendicular to the direction of travel. Therefore, charged particles moving in magnetic fields travel in circles.

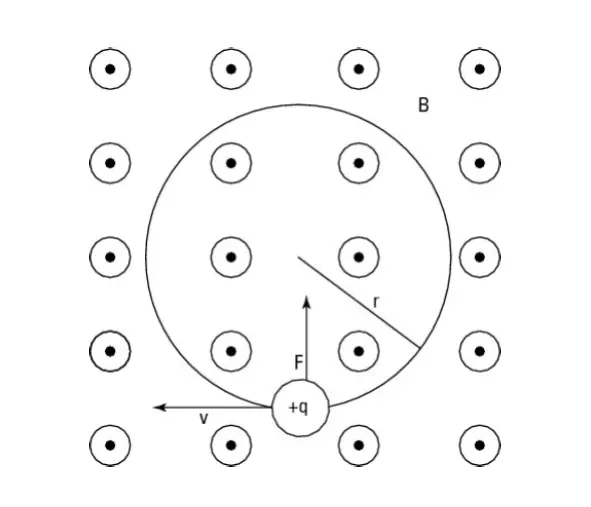
See Figure 2 to get the full picture. There, a positive charge is moving to the left in a magnetic field. The dots with circles around them tell us that magnetic field B is coming straight at us, out of the page. Using Fleming’s Left-Hand Rule, we can tell which way the resulting force goes – it is upward when the positive charge is at the location in Figure 2.

The charge responds to that upward force by moving upward. [check with Fleming’s Left-Hand Rule]
And because the force due to the magnetic field is always perpendicular to the direction of travel, the force changes direction, too.

Radius of orbit taken by the charged particle in a magnetic field – derivation

Here, we will derive the equation for the radius of the orbit of the charged particle moving in a magnetic field.
Because the force is always perpendicular to the direction of travel, it results in a circular motion.

You have the following equation for the force needed to keep an object in a circular motion: F = mv²/r

Here’s the magnitude of the force on a charged particle moving in a magnetic field: F = qvB sin θ

Because v is perpendicular to B in this case, θ equals 90°; therefore, sin θ equals 1, which means you get this: F = qvB

So we have to set the two force equations – for circular motion and for the charged particle in the magnetic field – equal to each other:
mv²/r = qvB

The radius of orbit taken by the charged particle in a magnetic field:
r = [mv]/[qB]

This equation gives you the radius of the charged particle’s path in a magnetic field, given its mass, charge, and velocity.