electrostatics – Worksheet 1 problem solution (Q2)

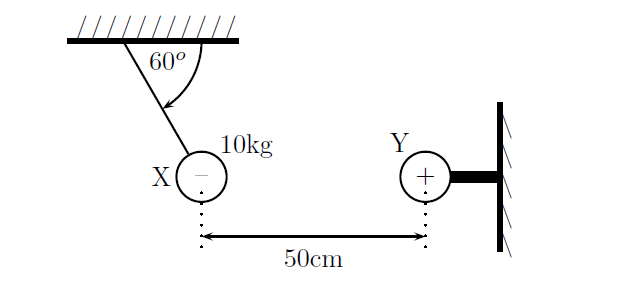
Question 2) In the picture below, X is a small negatively charged sphere with a mass of 10kg. It is suspended from the roof by an insulating rope which makes an angle of 60^o with the roof. Y is a small positively charged sphere that has the same magnitude of charge as X. Y is fixed to the wall by means of an insulating bracket.

Assuming the system is in equilibrium, what is the magnitude of the charge on X?

[ here is the complete worksheet: electrostatics worksheet 1 ]

Solution:

determining the charge on X – to determine their charges it’s required to know the force between X and Y & we can use Coulomb’s Law as we know the distance between them.

So, firstly, we need to determine the magnitude of the electrostatic force between X and Y.

The distance between X and Y is 50cm = 0.5m, and the mass of X is 10kg.

Draw the forces on X (with directions) and label.

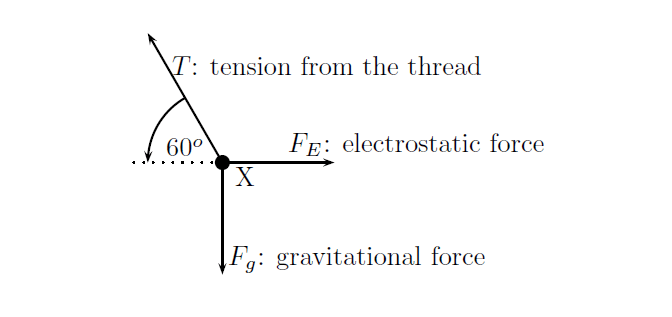
Determine the magnitude of the electrostatic force (F_E). Since nothing is moving (the system is in equilibrium) the vertical and horizontal components of the forces must cancel. Thus:

The only force we know is the gravitational force F_g = mg. Now we can calculate the magnitude of T from above:

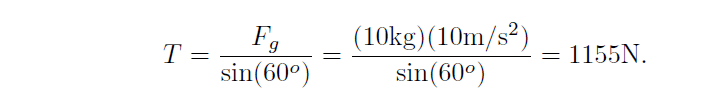
This means that F_E is:

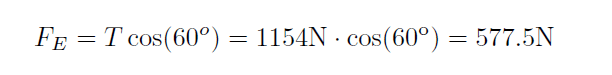
Now that we know the magnitude of the electrostatic force between X and Y, we can calculate their charges using Coulomb’s Law. Don’t forget that the magnitudes of the charges on X and Y are the same: |Q_X| = |Q_Y|. The magnitude of the electrostatic force is:

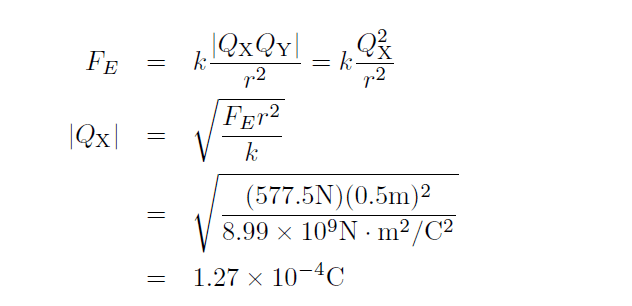
Thus the charge on X is -1.27 x 10^-4 C

[ here is the complete worksheet: electrostatics worksheet 1 ]