Thermal Conductivity – Numerical problems

Here, in this post, we will solve a bunch of numerical problems based on Thermal Conductivity. We have related posts on this that you can refer to if you want to revise the theory and formula derivation of thermal conductivity.

• Thermal conductivity – definition, values, significance, formula
• Thermal conductivity – derivation of formula, dimensional formula

Numerical problems on Thermal Conductivity

1 )

The thermal conductivity of copper is 390 W/m/K. Calculate the rate of heat flow through a copper bar whose area is 4.0 cm² and whose length is 0.50 m, if there is a temperature difference of 30°C maintained between its ends.

Solution:

2)

Find out the rate of flow of heat through a bar made of two materials in contact, as shown in the drawing below.

Let the thermal conductivity of B be 400 W/m/K while that for C is 50 W/m/K.

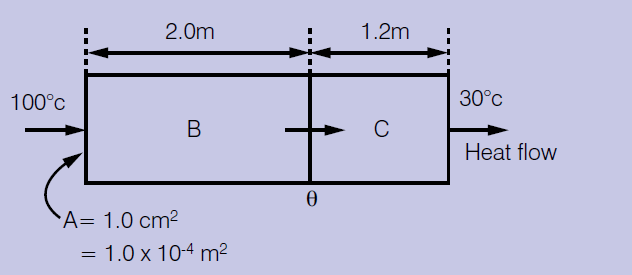
Solution:

Start by finding the temperature at the interface, θ say.
This rate must be the same through B and through C.

Equating them,

[400 x A x (100- θ)]/2 = [ 50 x A x ( θ -30)]/1.2

=> solving we get θ = 88°C.

Now to get the rate of flow, we will substitute θ = 88°C into the flow equation for either bar.

Thus, considering bar B, rate of flow of heat = [400 x A x (100- θ)]/2 = [400 x 1×10^-4 x (100- 88)]/2 = 0.24 W