Force constant k when Springs are in series and parallel

In this post, we will find more about spring constant or Force constant k and how to find out its value when Springs are in series and parallel.

---

Spring constant or force constant k

In Hooke’s law, we find a constant k which is known as force constant or stiffness constant. Robert Hooke discovered that the extension, x, of some objects (e.g. most wires and springs) is proportional to the load or force applied, F.
He wrote this as F = kx, where F = force in N, x = extension in m, and k = force constant in Nm^–1.

k is the force constant (or stiffness constant). Force constant is the force needed to extend an object that obeys Hooke’s law by 1 m. It depends on the material that the object is made from, as well as its length and shape. For springs, k in the formula F = kx is usually called the spring stiffness or spring constant.

Hooke’s law also applies in case of a pair of opposite forces

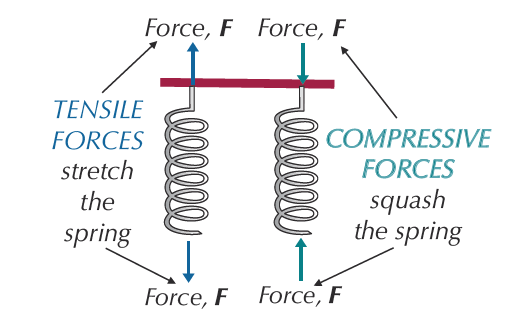
A metal spring also changes length when you apply a pair of opposite forces. The extension or compression of a spring is proportional to the force applied – so Hooke’s law not only applies for a single force but also it applies when there are a pair of opposite forces.

For springs, k in the formula F = kx is usually called the spring stiffness or spring constant.

Hooke’s law works just as well for compressive forces as tensile forces. For a spring, k has the same value whether the forces are tensile or compressive (though this isn’t true for all materials).

Equivalent force constant

If a force is applied to more than one spring (or wire), you can combine the force constants of the individual objects to find the overall combined force constant or Equivalent force constant of the system. You can then treat the system as one spring with force constant k. How you combine the force constants depends on how the springs are arranged.

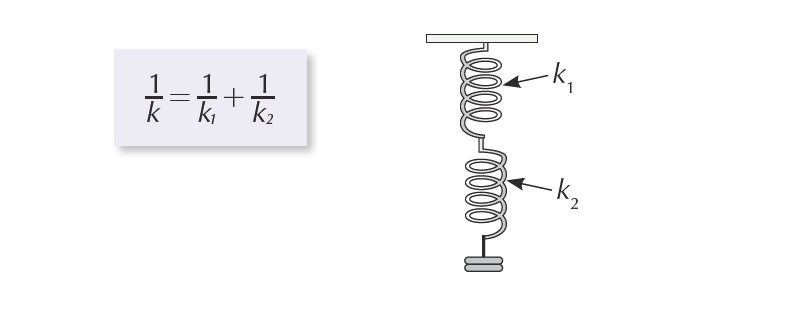
Equivalent force constant when Springs are in series

When Springs are in series, the reciprocal of the equivalent force constant is equal to the sum of the reciprocals of the individual force constants.

Say, k is the equivalent force constant when two springs of spring constant (or force constant) k₁ and k₂ respectively are arranged in series. Then the value of k is found using the following formula:
1/ k = 1/ k₁ + 1/k₂

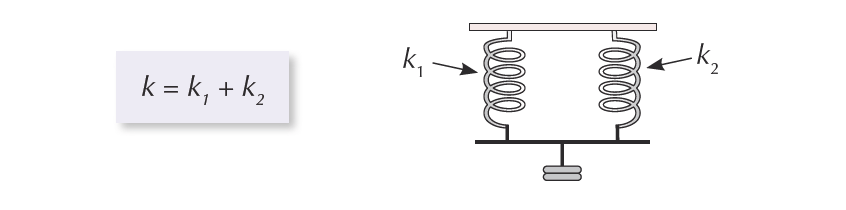
Equivalent force constant when Springs are in parallel

When Springs are in parallel, the equivalent force constant is just the sum of the force constants of the individual springs.

Say, k is the equivalent force constant when two springs of spring constant (or force constant) k₁ and k₂ respectively are arranged in parallel. Then the value of k is found using the following formula:
k = k₁ + k₂

Summary:

Equivalent force constant or Equivalent Spring constant when Springs are in series: 1/ k = 1/ k₁ + 1/k₂

Equivalent force constant or Equivalent Spring constant when Springs are in parallel: k = k₁ + k₂