How to solve Numerical problems based on Coulomb’s Law
Last updated on May 23rd, 2023 at 11:25 am
In this post, we will solve a few numerical problems using Coulomb’s law in a step-by-step approach. Before that, we will quickly revise this law and the equation related to this law. We require this equation of Coulomb’s Law to solve the numerical problems.
Electrostatic Force & Coulomb’s Law
Like charges repel each other while unlike charges attract each other. If the charges are at rest then the force between them is known as the electrostatic force.
The electrostatic force between charges increases when the magnitude of the charges increases or the distance between the charges decreases.
The electrostatic force was first studied in detail by Charles-Augustin de Coulomb around 1784. Through his observations, he was able to show that the magnitude of the electrostatic force between two point-like charges is inversely proportional to the square of the distance between the charges. He also discovered that the magnitude of the force is proportional to the product of the charges. That is:
F α Q1Q2/r2
where Q1 and Q2 are the magnitudes of the two charges respectively and r is the distance between them. The magnitude of the electrostatic force between two point-like charges is given by Coulomb’s law.
Definition: Coulomb’s law
Coulomb’s law states that the magnitude of the electrostatic force between two point charges is directly proportional to the product of the magnitudes of the charges and inversely proportional to the square of the distance between them.
F =kQ1Q2/ r2 ,
The proportionality constant k is called the electrostatic constant and has the value: 9.0 × 109 N·m2·C−2 in free space.
Numerical Problem – step-by-step solution using Coulomb’s Law
1) Two point-like charges carrying charges of +3 × 10−9 C and −5 × 10−9 C are 2 m apart. Determine the magnitude of the force between them and state whether it is attractive or repulsive.
SOLUTION
Step 1: Determine what is required
We are required to determine the force between two point charges given the charges and the distance between them.
Step 2: Determine how to approach the problem
We can use Coulomb’s law to calculate the magnitude of the force. F =kQ1Q2/ r2
Step 3: Determine what is given
We are given:
• Q1 = +3 × 10−9 C
• Q2 = −5 × 10−9 C
• r = 2 m
We know that k = 9.0 × 109 N·m2·C−2.
We can draw a diagram of the situation.
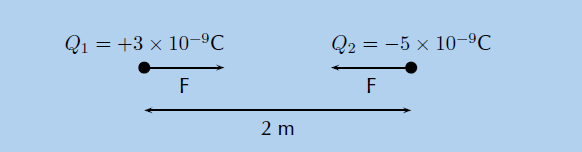
Step 4: Check units
All quantities are in SI units.
Step 5: Determine the magnitude of the force
Using Coulomb’s law we have
F =kQ1Q2/ r2
= ( 9.0 × 109)(3 × 10−9) (5 × 10−9)/22
= 3.37 × 10−8 N
Thus the magnitude of the force is 3.37 × 10−8 N. However since the point charges have opposite signs, the force will be attractive.
Step 6: Free body diagram
We can draw a free-body diagram to show the forces. Each charge experiences a force with the same magnitude and the forces are attractive, so we have:
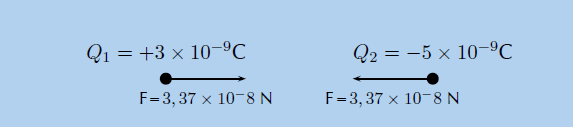
Reference: grade 11 phy sciences siyavula
