Mechanical properties of solids – Class 11 Notes
Last updated on May 22nd, 2023 at 12:35 pm
In this post, we will study the Mechanical properties of solids Class 11 Notes. This covers Hooke’s Law and the Modulus of Elasticity. On the way, we will learn two more terms: stress and strain. Finally, we will cover (a) Young’s Modulus (2) Shear Modulus (3) Bulk modulus. So let’s start.
Stress
To understand Hooke’s Law it’s mandatory to understand 2 terms: Stress and Strain. Let’s get some idea about those.
Let a force is applied to a body that can modify the shape and size of the object. Let’s call that Deforming Force F. As per Newton’s 3rd Law, a restoring force (say F1) will be generated inside which is equal to but opposite of the deforming force.
F1 = -F. Here F is the action and F1 is the reaction force.
The restoring force per unit area is called stress.
Considering only the magnitude of the restoring force, we can write the expression of stress as:
Stress = F / A, where A = area of cross-section of the body where action-reaction forces are being applied.
Its unit in SI is Newton/meter2 or Pascal.
Stress and Strain
A solid may change its dimensions in 3 different ways, resulting in 3 types of stress and strain: (1) Longitudinal stress & Longitudinal strain (2) Shearing stress, & shearing strain, and (3) Hydraulic stress & Volume strain
Tensile and Compressive stress (Longitudinal stress)
Here forces are applied at a right angle to the cross-sectional area or surfaces to either elongate or compress the object. That means these forces tend to cause a change in the length of the solid body and generate Longitudinal Stress. As said this stress may be of 2 types, tensile and compressive.
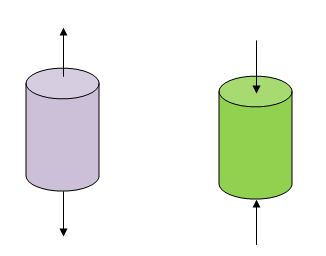
Tensile stress tends to enhance the length and compressive stress tries to decrease the length.
Longitudinal Stress = Force applied / area of the surface = F/A
Longitudinal Strain
Say the original length is L and the change in length is l. Here comes the term Longitudinal Strain which is stated as the change in length per unit length.
So Longitudinal Strain = l/L……………………..(1)
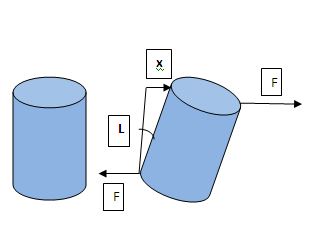
Tangential or Shearing Stress
If 2 equal and opposite deforming forces are applied parallel to the cross-sectional area of a cylinder-like object, then there is a relative displacement between the opposite faces of the cylinder.
In this case, the restoring force per unit area due to the applied tangential force is called tangential or shearing stress.
Shearing stress = F/A.
Shearing Strain
The strain related to shearing stress is called shearing strain. In the diagram, 2 equal, opposite, and parallel forces with magnitude F cause a relative displacement x between the opposite faces of the cylinder.
And during this displacement, an angle θ is generated between the original and displaced sidelines.
Here Shearing Strain = x/L = tan θ. ………………… (2)
If this angle θ is too small, then tan θ = θ ……………. (3)
so from (2 & 3), Shearing Strain = x/L = θ ……………….(4)
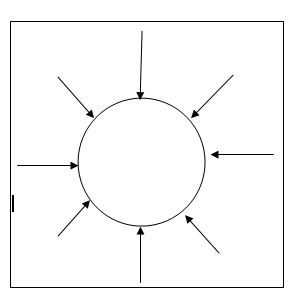
Hydraulic Stress
When a solid (say sphere) is placed in a fluid under high pressure and compressed uniformly on all sides, then the force applied by the fluid acts in a perpendicular direction at each point of the surface.
This is called Hydraulic Compression. This leads to a decrease in volume.
The internal restoring force per unit area is called Hydraulic Stress.
Hydraulic stress = F/A = hydraulic pressure.
Volume Strain
Related strain is called volume strain which is the ratio of change in volume and initial volume.
Volume Strain = Δv / V …………………. (5)
Next, we will state and discuss Hooke’s Law.
Hooke’s Law
Hooke’s Law of Elasticity states that: For small deformations, stress is directly proportional to strain.
Stress ∝ strain
So, Stress = K. Strain [ Hooke’s Law Equation about the stress-strain relationship ] ……………………. (a)
Here K is a constant.
Modulus of Elasticity
From equation (a) we get, Stress/Strain = K ……………………. (b)
This K is a proportionality constant called the Modulus of Elasticity.
From equation b, we can say that the Modulus of Elasticity is the ratio of Stress and Strain.
Now considering 3 different types of stress for solids, we have 3 different sets of elasticity modulus.
They are (a) Young’s Modulus (2) Shear Modulus (3) Bulk modulus
3 different sets of elasticity modulus
There are 3 types of elasticity modulus and they are:
- Young’s Modulus
- Shear Modulus
- Bulk Modulus
Let’s discuss these in detail here.
Young’s Modulus
Young’s Modulus is the ratio of Longitudinal Stress and Longitudinal Strain. If it’s designated with Y then
Y = Longitudinal Stress / Longitudinal Strain = (F/A)/(l/L) = (FL)/(Al)
Its unit is N/m2 or Pascal. Please note that Strain is dimensionless. See how to solve a numerical problem based on Young’s modulus.
Shear Modulus
Shear Modulus is the ratio of Shear Stress and Shear Strain. This is also known as the Modulus of Rigidity.
If it’s designated as G then
G = (F/A)/(x/L) = (F/A)/θ = F/(Aθ).
Bulk Modulus
Bulk Modulus (B)is the ratio of Hydraulic Stress and Volume Strain.
B = (F/A)/(Δv / V) = – P /(Δv / V)
Here P is the pressure. As the change in volume is indirectly proportional to the pressure applied, that’s why the negative sign is used.
Related study
Know about the Fundamentals of elasticity: Elasticity
Also, know about the extension-load graph here: Extension-load graph of spring & with analysis
And, this post will help you to understand Poisson’s ratio, strain energy & thermal stress: Poisson’s ratio & strain energy

