Buoyancy

Last updated on June 24th, 2023 at 03:11 pm

In this post, we will study the concepts of Buoyancy. We will start with some common examples to understand the phenomenon, and then define it and its related terms like Buoyant force. We will also explain Buoyancy and Buoyant force and derive related formulas.

Buoyancy meaning | What do you mean by Buoyancy

We have certainly experienced Buoyancy knowingly or unknowingly.

• When we try to place a mug in a bucket of water we feel one opposing force coming upwards from water as we push the mug inside the water. Buoyancy is synonymous with that upward push provided by the fluid (liquid water in this case).
• Similarly, when we place a rubber ball in a bucket of water we find the ball to float. We also see that a large part of the ball is above the surface of the water, and the rest of the ball is inside the water.
• Now if we push that rubber ball downwards, a larger part of the ball goes inside the water. But as we remove the force we are exerting, the ball comes upwards and floats again. That means to keep the ball inside the water at rest, we have to maintain a downward force on it continuously.
• To take the ball deeper, we have to exert more force until a large enough force downward on the ball gets it completely immersed.

We will now discuss buoyancy in detail. In this topic, we will discuss it with examples and get its definition and related equations. We also discuss the contribution of Archimedes in this regard.

Buoyancy Definition | Define Buoyancy

When an object is partially or completely immersed in a fluid, the fluid exerts a net upward force on it. This force is referred to as buoyant force and this phenomenon is known as buoyancy.

Buoyancy Force | Buoyant Force

The net upward force exerted by the fluid when an object is partially or completely immersed in that fluid is referred to as buoyant force or Buoyancy Force.

Now, what is the magnitude of this force? We will find it now by deriving the Buoyant force formula.

 Generation of the buoyant force | How does buoyant force generate?

To understand this let’s consider a cubical block immersed in a fluid of density ρ as in Figure 1.

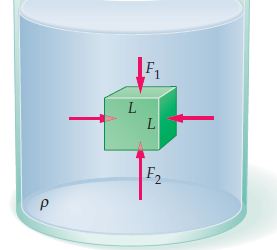
The surrounding fluid applies normal forces on all of its faces. Here we are assuming that you are aware of these 2 equations.

1) Force = Pressure X Area of application ………….. (1)
2) Pressure at a certain depth h inside a fluid of density ρ is equal to Atmospheric pressure + fluid pressure at that point= P(atm) + h ρ g. [ g is the acceleration due to gravity].

If we consider the pressure component inside fluid at depth h which is caused by the fluid column only then it is expressed as P = h ρ g …………. (2)

Coming back to the diagram, obviously, the horizontal forces pushing to the right and to the left faces of the block are equal (and opposite as well), hence they cancel each other and have no effect on the block.

But this doesn’t happen in the case of the vertical forces.

Note that the upward force exerted on the lower face is more than the downward force exerted on the upper face. Why?

The pressure at the lower face is greater than that at the upper face as Pressure is directly proportional to the depth here (See equation 2 above) and the lower face is deeper than the upper one. 

Also, you know from Equation 1 that Force is directly proportional to pressure.

Hence upward force on the lower face is more than the downward force on the upper face. This difference in forces gives rise to a net upward force—the buoyant force.

The magnitude of the buoyant force (deriving Buoyant force formula)

Let’s calculate the buoyant force acting on the block. First, we assume that the length of a side of the cubical block is L.

If pressure P1 exerted by the fluid on the top surface of the block causes the downward force F1 on the block, then,

F1 = P1 * A = P1 *  L^2 ………………… (3)
Note that we have used the fact that the area(A) of a square face of side L is L^2.

Let’s consider the bottom face. The bottom face is at a higher depth than the upper face. And the difference of depth = side of the block = L.

So the pressure at the lower face is given as:
P2 = P1 + ρgL ……………. (4)

[ You can clearly see this difference is caused only by the difference of their depths which is equal to L here]

Therefore, the upward force exerted on the bottom face of the cube is

F2 = P2 * A = (P1 + ρgL)* L^2 = P1L^2 + ρgL^3 = F1 + ρgL^3 …………………. (5)

If we take upward as the positive direction, the net vertical force exerted by the fluid on the block—that is, the buoyant force causing Buoyancy can be expressed as

Fb = F2 – F1 = ρ g L^3.……………………………(6)

Now see the expression or equation of buoyant force. It’s ρ g L^3.

Now L^3 is the volume of the cube immersed = volume of the fluid displaced (as certainly, the immersed volume of the cube has displaced an equal volume of the fluid to make its own place.)

As we know mass = volume * density, so ρ * L^3 is the mass of the displaced fluid.

And as we know weight = mass * g, so ρ L^3 *g is the weight of the displaced fluid.

Buoyant force formula | Buoyancy force formula

Buoyancy causes an upward buoyant force that is equal to the weight of the displaced fluid.
The magnitude of Buoyant force = ρ g V
where ρ is the density of the fluid, V is the volume of the fluid displaced, g is the acceleration due to gravity

Archimedes’ Principle

This is a special case of Archimedes’ principle: An object completely immersed in fluid experiences an upward buoyant force equal in magnitude to the weight of the fluid displaced by the object.