Different types of Numbers (definition & example)
In this post, we have compiled information about different types of numbers (definition, examples, etc.)
What are Fibonacci numbers?
Fibonacci numbers are a series of numbers where each, after the second term, is the sum of the two preceding numbers—for example, 1, 1, 2, 3, 5, 8, 13, 21, and so on). They were first described by Leonardo Fibonacci (c. 1180–c. 1250), also known as Leonard of Pisa, as part of a thesis on series in his most famous book Liber abaci (The Book of the Calculator), published in 1202 and later revised by him.
Fibonacci numbers are used frequently to illustrate natural sequences, such as the spiral organization of a sunflower’s seeds, the chambers of a nautilus shell, or the reproductive capabilities of rabbits.
What is a prime number presently known?
A prime number is one that is evenly divisible only by itself and 1. The integers 1, 2, 3, 5, 7, 11, 13, 17, and 19 are prime numbers.
What is a perfect number?
A perfect number is a number equal to the sum of all its proper divisors (divisors smaller than the number) including 1. The number 6 is the smallest perfect number; the sum of its divisors 1, 2, and 3 equals 6. The next three perfect numbers are 28, 496, and 8,126. No odd perfect numbers are known. The largest known perfect number is
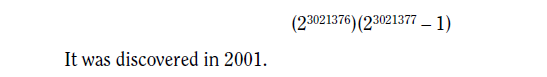
How large is a googol?
A googol is 10100 (the number 1 followed by 100 zeros). Unlike most other names for numbers, it does not relate to any other numbering scale.
The American mathematician Edward Kasner (1878–1955) first used the term in 1938; when searching for a term for this large number, Kasner asked his nephew, Milton Sirotta (1911–1981), then about nine years old, to suggest a name. The googolplex is 10 followed by a googol of zeros, represented as 10googol. The popular Web search engine Google.com is named after the concept of a googol.
What is an irrational number?
Numbers that cannot be expressed as an exact ratio are called irrational numbers; numbers that can be expressed as an exact ratio are called rational numbers.
For instance, 1/2 (one half, or 50 percent of something) is rational; however, 1.61803 (fi), 3.14159 (pi), 1.41421 (square root of 2 ), are irrational. History claims that Pythagoras in the sixth century B.C.E. first used the term when he discovered that the square root of 2 could not be expressed as a fraction.
What are imaginary numbers?
Imaginary numbers are the square roots of negative numbers. Since the square is the product of two equal numbers with like signs it is always positive. Therefore, no number multiplied by itself can give a negative real number. The symbol “i” is used to indicate an imaginary number.
What are some examples of numbers and mathematical concepts in nature?
The world can be articulated with numbers and mathematics. Some numbers are especially prominent. The number six is ubiquitous: every normal snowflake has six sides; every honeybee colony’s combs are six-sided hexagons. The curved, gradually decreasing chambers of a nautilus shell are propagating spirals of the golden section and the Fibonacci sequence of numbers. Pine cones also rely on the Fibonacci sequence, as do many plants and flowers in their seed and stem arrangements. Fractals are evident in shorelines, blood vessels, and mountains.
