Coordinate Systems & different types of Coordinate Systems

To specify the location of a point in space, a coordinate system must be used. A coordinate system consists of a reference point called the origin O and a set of labeled axes. The positive direction of an axis is in the direction of increasing numbers, whereas the negative direction is the opposite.

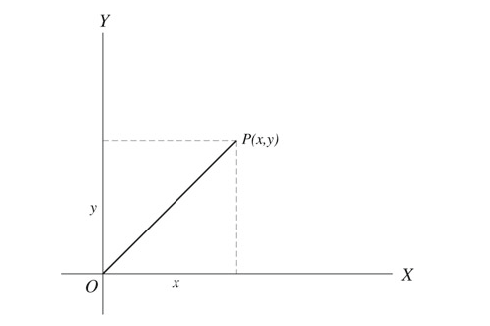
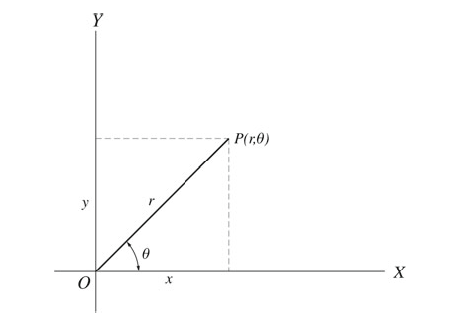
different types of Coordinate Systems in 2 dimensions

Figures 1 and 2 show the rectangular (or Cartesian) coordinate system and the polar coordinates of a point, respectively.

The rectangular coordinates x and y are related to the polar coordinates r and θ by the following relations:

x = r cos θ
y = r sin θ
tan θ = y/x
r = √(x² + y²)

**figure 1: The rectangular (cartesian) coordinate system**

**figure 2: The polar coordinate system**

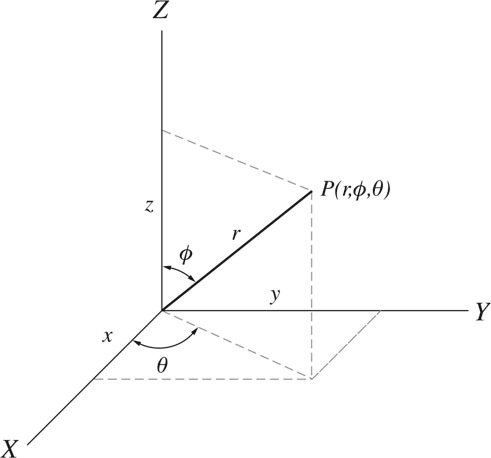
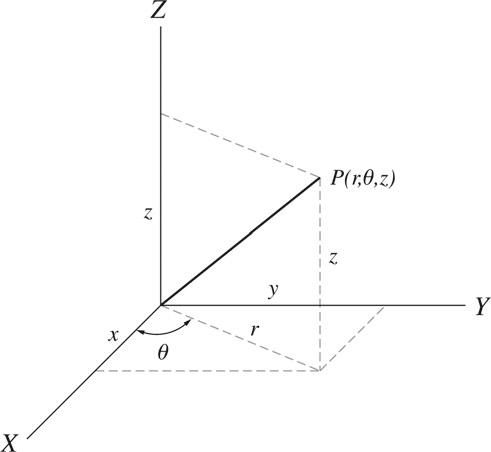
different types of Coordinate Systems in 3 dimensions – with diagram

In three dimensions, the cartesian coordinate system is shown in Fig. 3.

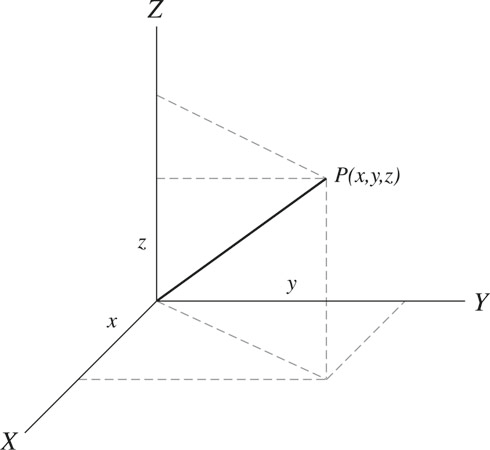
**figure 3: The cartesian coordinate system in three dimensions**

Other used coordinate systems in three dimensions are the spherical and cylindrical coordinates (Figs. 4 and 5).

**figure 4: The spherical coordinate system**

**figure 5: The cylindrical coordinate system**