Estimation of physical quantities with Significant Figures and Order of Magnitude

Estimation of physical quantities brings in the concepts of Significant Figures and Order of Magnitude. It is always a good idea to be able to estimate the size of a quantity so that when you work out a problem or finish an experiment you have a rough idea of what sort of value to expect. Physicists use the phrase ‘the right order of magnitude’ to refer to a number in the right sort of range.

Scientific Notation: A Matter of Convenience

Scientific notation is a way of writing numbers that are too big or too small in a convenient and standard form. In other words, Scientific notation is a less wordy way to write very large and very small numbers.

Scientific notation has a number of useful properties and is commonly used in calculators and by scientists, mathematicians, and engineers. In scientific notation, all numbers are written in the form of p⋅10^q (p multiplied by ten raised to the power of q), where the exponent q is an integer, and the coefficient p is any real number.

Most of the interesting phenomena in our universe are not on the human scale. It would take about 1,000,000,000,000,000,000,000 bacteria to equal the mass of a human body. See how difficult and time-consuming it would be to write an exact number of zeroes if you follow this way of notation. Scientific notation is opted to avoid this kind of situation to get a less awkward and wordy way to write very large and very small numbers such as these.

A simple system of scientific Notation

The scientific notation means writing a number in terms of a product of something from 1 to 10 and something else that is a power of ten.

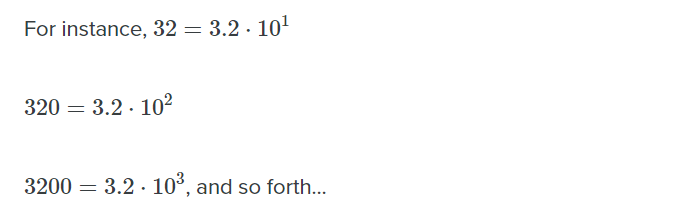
Round-off Error

A round-off error, also called a rounding error, is the difference between the calculated approximation of a number and its exact mathematical value. When a sequence of calculations subject to rounding errors is made, errors may accumulate, sometimes dominating the calculation.

Calculations rarely lead to whole numbers. As such, values are expressed in the form of a decimal with infinite digits. The more digits that are used, the more accurate the calculations will be upon completion. Using a slew of digits in multiple calculations, however, is often unfeasible if calculating by hand and can lead to much more human error when keeping track of so many digits. To make calculations much easier, the results are often ’rounded off’ to the nearest few decimal places.

For example, the equation for finding the area of a circle is A=πr^2. The number π (pi) has infinitely many digits but can be truncated to a rounded representation of as 3.14159265359. However, for the convenience of performing calculations by hand, this number is typically rounded even further, to the nearest two decimal places, giving just 3.14. Though this technically decreases the accuracy of the calculations, the value derived is typically ‘close enough’ for most estimation purposes.

However, when doing a series of calculations, numbers are rounded off at each subsequent step. This leads to an accumulation of errors, and if profound enough, can misrepresent calculated values and lead to miscalculations and mistakes.

The following is an example of round-off error:

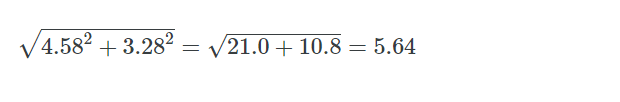
Rounding these numbers off to one decimal place or to the nearest whole number would change the answer to 5.7 and 6, respectively. The more rounding off that is done, the more errors are introduced.

Orders of Magnitude

Order of Magnitude is the class of scale or magnitude of any amount, where each class contains values of a fixed ratio (most often 10) to the class preceding it. For example, something that is 2 orders of magnitude larger is 100 times larger; something that is 3 orders of magnitude larger is 1000 times larger; and something that is 6 orders of magnitude larger is one million times larger, because 10^2 = 100, 10^3 = 1000, and 10^6 = one million

An order of magnitude is the class of scale of any amount in which each class contains values of a fixed ratio to the class preceding it. In its most common usage, the amount scaled is 10, and the scale is the exponent applied to this amount (therefore, to be an order of magnitude greater is to be 10 times, or 10 to the power of 1, greater). Such differences in order of magnitude can be measured on the logarithmic scale in “decades,” or factors of 10. It is common among scientists and technologists to say that a parameter whose value is not accurately known or is known only within a range is “on the order of” some value. The order of magnitude of a physical quantity is its magnitude in powers of ten when the physical quantity is expressed in powers of ten with one digit to the left of the decimal.

Orders of magnitude are generally used to make very approximate comparisons and reflect very large differences. If two numbers differ by one order of magnitude, one is about ten times larger than the other. If they differ by two orders of magnitude, they differ by a factor of about 100. Two numbers of the same order of magnitude have roughly the same scale — the larger value is less than ten times the smaller value.

Reference: lumen learning