Path of light is reversible – Principle of Reversibility of light

Last updated on April 14th, 2021 at 04:59 pm

If a ray of light travel from medium 1 to medium 2 along a certain path, it retraces the path, when it passes from medium 2 to medium 1. Thus the path of light is reversible. And this principle is known as the principle of reversibility of light.

Here we also derive the relationship equation between the refractive index values of 2 media in contact applying the concept of Principle of Reversibility of light

Relationship between refractive index values of 2 media in contact – Application of Principle of Reversibility

Let’s derive the relationship equation between the refractive index values of 2 media in contact applying the concept of Principle of Reversibility of light.

Let’s say AB is the refracting surface separating the two media. MN is normal on AB.

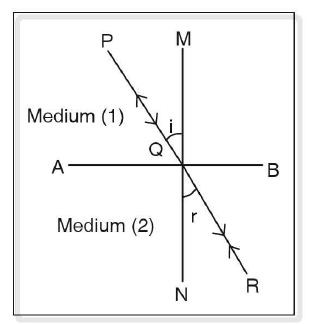
A ray of light PQ is obliquely incident at an angle i and is refracted along QR at an angle r.
Refractive index of medium 2 with respect to medium 1 is ₁µ₂ = sin i / sin r ………………. (1)

When a ray of light travels from medium 2 to medium 1, according to the principle of reversibility, RQ is the incident ray and QP is the refracted ray.

In this case, angle r is acting as the angle of incidence and angle i is the angle of refraction.
So, from here we can formulate the refractive index of medium 1 with respect to medium 2 in this way:
₂µ₁ = sin r / sin i ………………. (2)

So from (2) and (1) we get, ₂µ₁ = sin r / sin i = 1/(sin i / sin r) = 1/ ₁µ₂
=> ₂µ₁ = 1/ ₁µ₂

This is relationship between the refractive index values of 2 media in contact derived from the Principle of Reversibility of light.