Moment of Couple & its Formula
Last updated on April 20th, 2023 at 02:21 am
Moment of Couple – this term in physics is based on an understanding of 2 concepts, the first one is ‘moment’ and the second one is ‘couple’. The moment in physics denotes the turning effect. A couple in physics is discussed in our post on Couple – you can read it here.
Moment of Couple
Here, we will define the moment of a couple, and derive its formula as well.
Moment of Couple – definition
The moment of Couple is the cumulative turning effect produced by a ‘couple’ of forces and its magnitude is the product of either force of the couple and the perpendicular distance between the two forces of the couple (or couple arm length).
derivation of the Moment of Couple formula
Say, Two forces F and −F, having the same magnitude, parallel lines of action, and opposite directions, have formed a couple.
Let us denote the position vectors of the points of application of F and – F by rA and rB, respectively. The moment M of the couple about O is the sum of the moments of F and of −F about O.
The sum of the moments of the two forces about O is:
rA × F + rB ×(−F)=(rA − rB)×F
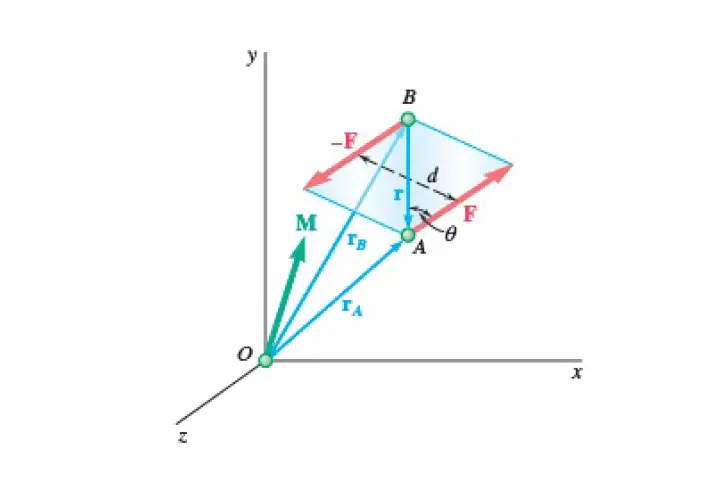
Setting rA − rB = r, where r is the vector joining the points of application of the two forces, we conclude that the sum of the moments of F and −F about O is represented by the vector M = r × F
The vector M is called the moment of the couple. It is perpendicular to the plane containing the two forces, and its magnitude is M = r F sin θ = F d, where d is the perpendicular distance between the lines of action of F and −F, and θ is the angle between F (or −F) and r. The direction of M is defined by the right-hand rule.
Moment of couple Formula
The magnitude of Moment of Couple = Magnitude of either force of the couple x couple arm length
