Equilibrium of a rigid body-conditions and physics
Last updated on September 17th, 2021 at 09:47 am
A rigid body is said to be in mechanical equilibrium if both its linear momentum and angular momentum are not changing with time. In other words, the body is in mechanical equilibrium when it has neither linear acceleration nor angular acceleration. For a body of finite size to be in equilibrium:
(i) the resultant force on the body must be zero
(ii) the resultant torque on the body must be zero
Conditions for Equilibrium
Here are the two conditions for equilibrium and their respective equations.
(1) The total or net force i.e. the vector sum of all the forces, on the rigid body is zero.
i.e., ΣFi = 0 when i=1 to n …………………… (1 a)
or
dptot/dt = 0 where ptot=net linear momentum………………… (1b)
(2) The total Torque i.e. the vector sum of the torques on the rigid body is zero.
ΣΤi = 0 when i=1 to n………………….. (2a)
or
dLtot/dt = 0 where Ltot=net angular momentum…………………(2b)
Conditions for mechanical equilibrium
Expanding equation 1a and 2a:
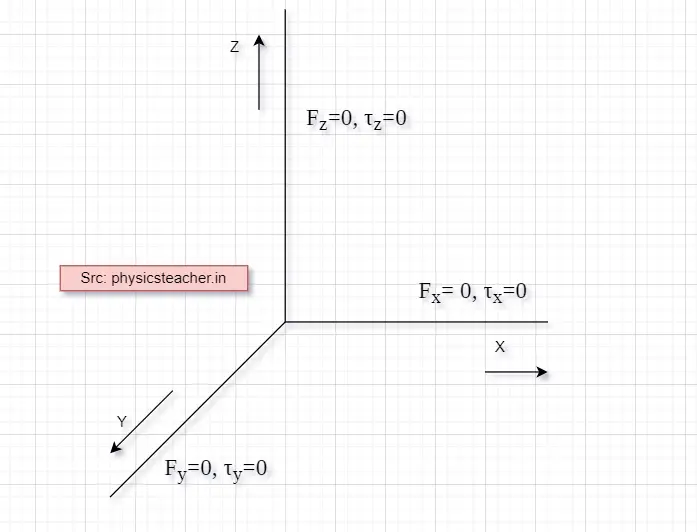
1) ΣFix = 0 when i=1 to n => Net force along X axis = Fx = 0
2) ΣFiy = 0 when i=1 to n => Net force along Y axis = Fy = 0
3) ΣFiz = 0 when i=1 to n => Net force along Z axis = Fz =0
4) ΣΤix = 0 when i=1 to n => Net torque along X axis = τx=0
5) ΣΤiy = 0 when i=1 to n => Net torque along Y axis =τy=0
6) ΣΤiz = 0 when i=1 to n => Net torque along Z axis =τz=0
For mechanical equilibrium, these 6 independent conditions are to be satisfied.
[ Related study: Read this post on the equilibrium of leaning ladder & numerical ]
Conditions for equilibrium when forces are coplanar
We need only 3 conditions to be satisfied for this when the forces working on the rigid body are coplanar.
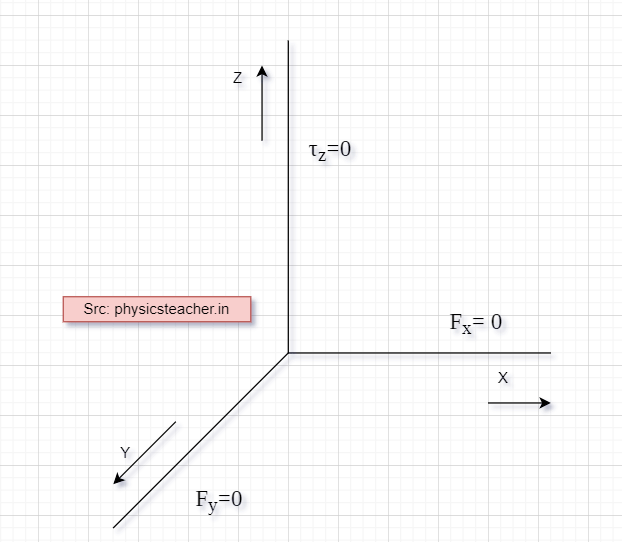
* Two of these conditions correspond to translational equilibrium: The sum of forces along any 2 perpendicular axes in the plane must be zero. so if we take x and y axes, then ΣFx = 0 ΣFy = 0
* The third condition is about Rotational Equilibrium: The sum of the torques along any axis perpendicular to the plane of the above-said forces must be zero. Here it will be: ΣΤz = 0
Principle of moments and rotational equilibrium condition
The principle of moments is a restatement of the condition for a body to be in Rotational equilibrium.
For a body to be in rotational equilibrium, the sum of the moments about any point is zero.
A useful way of using this when you are considering coplanar forces is to say ‘the clockwise moments = the anticlockwise moments’.
Partial Equilibrium
A body may be in this Partial Equilibrium condition. It means that the body may be in translational equilibrium but not in rotational equilibrium and vice versa.
Case 1:
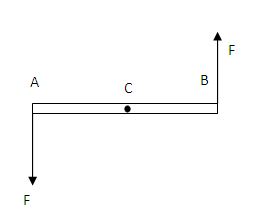
AB is a light rod and C is its midpoint. So CA = CB = r (say).
At A a force F is applied downwards and at B the same amount of force F is applied but in opposite direction.
Here from the diagram, it’s clear that the net force on the rod is zero. [ F + (-F) =0 ]
But what is the net Torque?
Say at point A the torque is T1 and at point B it’s T2.
T1= + F r. (Here, + denotes anticlockwise)
Similarly, T2 = + F r.
As both the torques are trying to move the rod anticlockwise, so certainly the net Torque on the rod is non-zero.
So in this case, the rod is in translational equilibrium (net force zero) but it’s not in rotational equilibrium. (net torque nonzero). That means it’s a case of Partial Equilibrium.
Case 2:
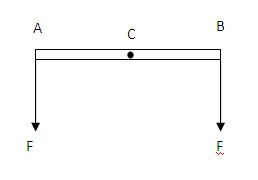
In this case, both the forces at point A and B are equal (F) like in case 1 but this time both are working in the same direction (downwards here). As a result, the net force is nonzero.
Let’s consider the torques now.
At A and B magnitudes of the applied torques are the same, i.e. r F. But in this case, their directions are opposite to each other.
At point A the torque tries to move the rod anticlockwise, at point B the torque plays clockwise.
Therefore, in this case, the net torque is zero.
So in this case, the rod is in rotational equilibrium (net torque zero) but it’s not in translational equilibrium. (net force nonzero). That means it’s another case of Partial Equilibrium.
Couple – Rotation without translation
A pair of equal and opposite forces with different lines of action is known as a couple.
A couple produces rotation without translation.
Example of the couple: When we open the lid of a bottle by turning it, we apply a couple to the lid through our fingers.
Conclusion
Dear Reader, Hope you have found this tutorial on the Equilibrium of a rigid body useful enough to share among your friends.
Also pls note that you are with physicsteacher.in – so please bookmark this site as well in your browser. See you soon on another page of this site.
Suggested Read:
